תקציר|
עבודת שורשים|מדריך למורה
בעקבות בחינת הבגרות לתלמידי 4 יחידות – 35481 – קיץ תשע"ו – מועד ב - שאלה 6
חלק א
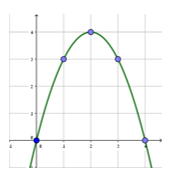
לפניכם גרף הפונקציה
1. מהו תחום ההגדרה של הפונקציה ?
2. מצאו את נקודות הקיצון המוחלט של הפונקציה f וקבעו את סוגן.
3. מה הקשר בין תחום העלייה של הפונקציה h לבין תחום העלייה של הפונקציה f? נסו להסביר את תשובתכם ביותר מאשר דרך אחת.
4. סרטטו באותה מערכת צירים את גרף הפונקציה .
היעזרו בנקודות המסומנות באדום. האם לכל אחת מהן יש נקודה מתאימה על גרף הפונקציה f?
5. על גרף הפונקציה h מסומנות בירוק שתי נקודות ששיעור ה- y שלהן הוא 1. הסבירו מדוע נקודות אלה נמצאו גם על גרף הפונקציה f?
(רמז: מה הקשר בין מספרים קטנים מ- 1 לבין השורשים הריבועיים שלהם?)
חלק ב
נתונה הפונקציה
1.מהו תחום ההגדרה של הפונקציה g?
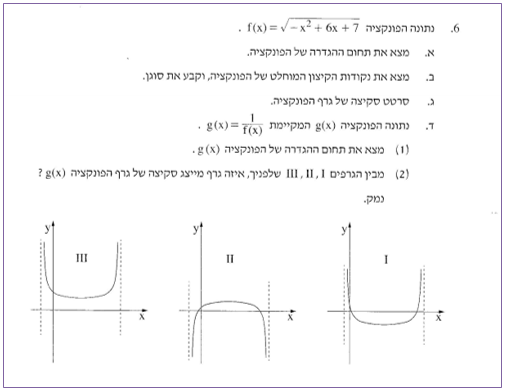
2. איזה מן הגרפים הבאים יכול לייצג סקיצה של גרף הפונקציה g? הסבירו.
חלק ג – סרטוט גרף של פונקציית שורש מורכבת בעזרת גרף הפונקציה הפנימית בלבד.
לפניכם גרף של פונקציה h.
נסרטט בעזרתו את גרף הפונקציה :
1. מהו תחום ההגדרה של הפונקציה f?
2. מצאו את נקודות הקיצון המוחלט של הפונקציה f וקבעו את סוגן.
3. מה הקשר בין תחום העלייה של הפונקציה h לבין תחום העלייה של הפונקציה f? נסו להסביר את תשובתכם ביותר מאשר דרך אחת.
4. סרטטו באותה מערכת צירים את גרף הפונקציה . היעזרו בנקודות המסומנות.
חלק ד – הרחבת החקירה לפונקציות נוספות מהמשפחה , כאשר h פונקציה ממעלה שנייה
היישומון שורשים מאפשר לסרטט גרפים של פונקציות שורש מורכבות, יחד עם פונקציה פנימית שהיא פונקציה ממעלה שנייה. משנים את הפרמטרים של הפונקציה הפנימית, והפונקציה המורכבת משתנה אף היא.
לנוחיות, נרשום את הפונקציה ממעלה שנייה בצורתה הקדקודית:
1. באיורים שלפניכם גרף הפונקציה הפנימית מופיע בקו רציף, וגרף הפונקציה המורכבת מופיע בקו מרוסק. מצאו באמצעות היישומון פונקציות שיכולות להתאים לאיורים:
2. הסבירו מדוע אין אפשרות לקבל ביישומון את צירוף הגרפים הבא:
(הגרף המקווקו הוא של הפונקציה המורכבת והגרף הרציף הוא של הפונקציה הפנימית)
היעזרו בסעיף 5 של חלק א'.
