לקפל פרבולה

תקציר| לקפל פרבולה 

הגדרה גיאומטרית:
פרבולה היא המקום הגיאומטרי של כל הנקודות שמרחקן מנקודה קבועה (המוקד) וישר קבוע (המדריך) שווה.

1. בעזרת קיפולים של דף נייר ונקודה אחת עליו נוכל ליצור באורח פלא פרבולה.
ללא סרגל, מחוגה או כל כלי מדידה...

על דף נייר: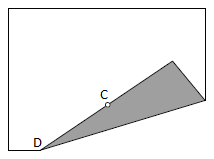 

-  סמנו נקודה C בקרבת אחת משפות הדף.
-  סמנו נקודה D על שפת הדף אליה התייחסתם קודם.
-  קפלו את הדף כך שהנקודה C תתלכד עם הנקודה D.
-  פתחו את הקפל וסמנו נקודה D אחרת על שפת הדף.
-  שוב קפלו את הדף כך שהנקודה C תתלכד עם הנקודה שסימנתם על שפת הדף.
-  חיזרו על התהליך עוד מספר פעמים.כדי לראות את התמונה שיוצרים הקפלים באופן ברור מומלץ לעבור עליהם בעזרת עפרון וסרגל.

מה קיבלתם?

- השוו את הנייר המקופל שלכם עם זה של חברכם. תארו את הדומה ואת השונה.

- קחו נייר נוסף, סמנו נקודה בתוכו במקום שונה וחזרו על התהליך. מה קיבלתם הפעם?

שאלות למחשבה:

א. ראינו כי הקיפולים יוצרים את המתאר של הפרבולה. מהם לדעתכם המוקד והמדריך?
ב. מה ניתן לומר על היחס הגיאומטרי בין הנקודות C,D וישר הקיפול ?
ג. מה ניתן לומר על ישר הקיפול ביחס לפרבולה ?
ד. אם נזיז את הנקודה C קרוב יותר לשפת הדף כיצד תשתנה הפרבולה? כיצד תשתנה הפרבולה אם נרחיק את הנקודה משפת הדף? 

 Thinking out loud 

2. לשחק בקיפולים:
בכדי להבין את הפלא ובכדי שנוכל לחקור מצבים שונים היעזרו ביישומון (קובץ גאוגברה להורדה).
א. גררו את הנקודה D והפעילו עקבות אחר הקיפולים. מה קיבלתם? מה ניתן לומר על כל קיפול ביחס לפרבולה? 
ב. בודאי שמתם לב כי הקיפול משיק לפרבולה, התוכלו לשער היכן נקודת ההשקה? כיצד נקודת ההשקה קשורה לנקודה D?
ג. צרו ביישומון פרבולות שונות על ידי שינוי מיקום הנקודה C.

1. כיצד תשתנה הפרבולה אם נמקם את C קרוב יותר לשפת הדף?
2. כיצד תשתנה הפרבולה אם נמקם את C רחוק יותר משפת הדף?
3. כיצד תשתנה הפרבולה אם נמקם את C על שפת הדף?
4. כיצד תשתנה הפרבולה אם נמקם את  C מתחת לשפת הדף?

3. כיצד נוכיח כי קיפולי הנייר יוצרים פרבולה?

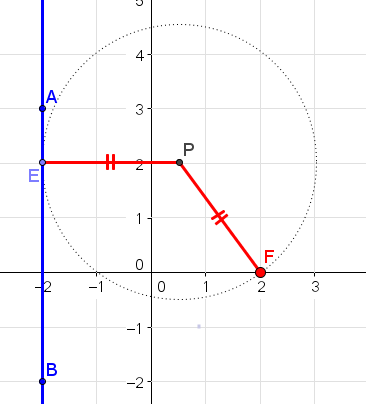
נתבונן באיור הבא המייצג את קיפולי הנייר של הפרבולה: 

א. הסבירו מדוע CM=MD.
ב. הקו המקווקו מייצג את קו הקיפול. מה תוכלו לומר עליו ביחס ל- CD?
ג. נבנה אנך לישר המייצג את שפת הדף דרך הנקודה D. הסבירו מדוע CP=DP .
ד. הראו על פי ההגדרה הגיאומטרית של הפרבולה כי הנקודה P על הפרבולה.
ה. ציינו מיהו המדריך ומיהי נקודת המוקד.

4. עוד משחקי פרבולה

לפניכם יישומון לבניית הפרבולה כמקום הגיאומטרי.

א. הסבירו איזו תכונה מקיימת הנקודה P ביחס לישר המדריך ולנקודת המוקד.
ב. קרבו והרחיקו את נקודת המוקד מהמדריך. כיצד תשתנה הפרבולה?
ג. שנו את מיקום המדריך באופנים שונים. כיצד תשתנה הפרבולה?
ד. צרו, אם ניתן, בעזרת היישומון את הפרבולות הבאות: y²=-x, y=x² , y²=x+1
מצאו את המוקד והמדריך של כל פרבולה

נקודה למחשבה:
כיצד יראה המקום הגיאומטרי אם המדריך לא יהיה ישר אלא מעגל?

מקורות נוספים:

• הפרבולה כצורה גיאומטרית – חמוטל דוד, על"ה 29.
• Famous Curves Index– מדור באתר The MT History of Mathematics archive ובו רשימת עקומים מפורסמים במתמטיקה עם הסבר היסטורי ומתמטי וכן יישומים דינאמיים מדגימים.
• אוגדן למורה: גיאומטריה אנליטית - פעילויות ממוחשבות – מחשבמטיקה, מכון וייצמן