- עמוד הבית
- משולשים
משולשים
תיאור: אוסף משימות קצרות שמטרתן לחדד, להעמיק את ההבנה ולעורר שיח מתמטי בכיתה. המשימות מתאימות לתלמידי כיתה ט' ברמות הגבוהות. השאלות הן שאלות העמקה בתכונות מרובעים ומשולשים המזמנות פיתוח מיומנויות הוכחה באמצעות המשפטים הנלמדים בתוכנית הלימודים של כיתה ט.
תיאור: דף הפעילות עוסק בקשר שבין טענות והיפוכן. הפעילות מזמנת שימוש באלגברה למטרת הוכחה, הן בטענות אלגבריות והן בטענות גאומטריות, וכן חיפוש דוגמאות נגדיות לשם הפרכה. נציין שהפרכה של טענות שגויות באמצעות דוגמאות נגדיות אינו המוקד העיקרי של הפעילות. לנושא של הפרכות תוקדש פעילות אחרת.
תיאור: מטרתה הראשונית של הפעילות "הכל זהב" היא לשמר ידע קודם מלימודי הגאומטריה לקראת נושאים מרכזיים שילמדו בהמשך. כך משלבת הפעילות נושאים בגאומטריה (דמיון משולשים וסכום זוויות במצולע) שהתלמידים רכשו בכיתה ח' ובתחילת כיתה ט' עם תוכן אלגברי ופתרון משוואות ריבועיות הנמצא בלב חומר הלימודים של כיתה ט' כאן גם פוגשים התלמידים משוואה ריבועית שפתרונותיה הם מספרים אי-רציונליים כזריעת זרעים לעתיד.
מקור: מרכז מורים ארצי למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
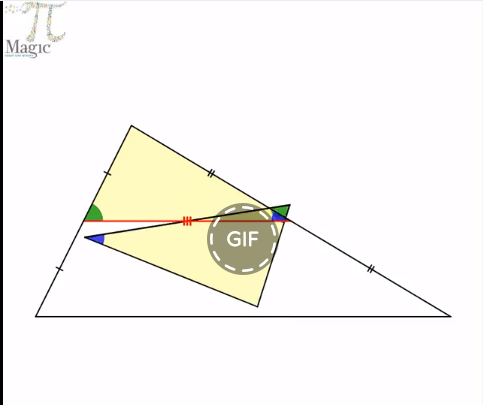
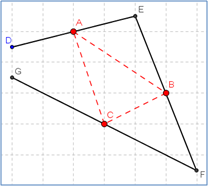
תאור: דף עבודה, יישום דינאמי - משולש לבעית חקר האם וכיצד ניתן לבנות משולש מנקודות אמצעי הצלעות. הבעיה גם מורחבת למרובעים וניתן לחקור בעזרתה יישום דינאמי - מרובע
מקור: אתר הפייסבוק של עידן טל
אופי הפעילות: תמונה דינאמית ממחישה ומעוררת דיון כיתתי
תיאור: התמונה הדינאמית מספקת בסיס להוכחה לתכונה של התיכון ליתר במשולש ישר זוית באמצעות הסתכלות על קטע אמצעים במשולש ועל מלבן שחסום בו.
גם אם סדר ההוראה המקובל אינו תואם הוכחה זו, ההקשרים הגיאומטריים המוצגים בתמונה הדינאמית יכולים לעורר מחשבה ודיון משמעותיים.
* אין לשכוח שתמונה דינאמית אינה מספקת הוכחה. יש להשלים הוכחה מדויקת בסיום הדיון שמתקיים בכיתה בעקבות הצפייה בתמונה הדינאמית.
מקור: אתר הפייסבוק של עידן טל
אופי הפעילות: תמונה דינאמית ממחישה ומעוררת דיון כיתתי
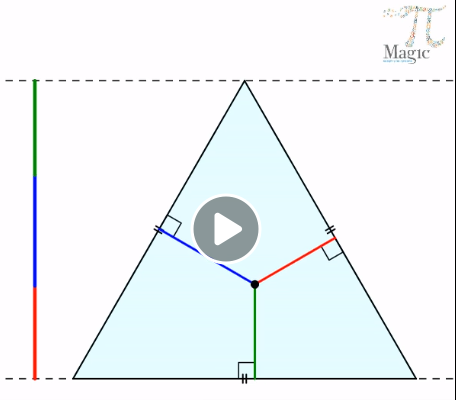
תיאור: התמונה ממחישה בתהליך דינאמי את השיוויון של סכום המרחקים של נקודה כלשהי בתוך משולש שווה צלעות מצלעותיו לאורך הגובה של המשולש.
התמונה לא מספקת הוכחה למשפט.
מקור: אתר הפייסבוק של עידן טל
אופי הפעילות: תמונה דינאמית ממחישה ומעוררת דיון כיתתי
תיאור: בתמונה הדינאמית מחולק משולש לארבעה משלושים חופפים, כך שניתן להסיק את תכונת קטע האמצעים. עוד ניתן לדבר על חפיפת משולשים, דמיון משולשים ומושגים קשורים.
* אין לשכוח שתמונה דינאמית אינה מספקת הוכחה. יש להשלים הוכחה מדויקת בסיום הדיון שמתקיים בכיתה בעקבות הצפייה בתמונה הדינאמית.
מקור: מרכז מורים ארצי למתמטיקה בחינוך העל יסודי
אופי הפעילות: חקר בעזרת יישום דינאמי
תאור: דף עבודה אינטראקטיבי ויישום דינאמי לדיון וחקירה של המשפט: הגובה במשולש ישר זווית שווה לממוצע הגיאומטרי של היטליו.
